Como fazer o cubo magico 4x4

Como fazer oCubo Magico 4x4? Certamente você já se perguntou como um cubo é resolvido 4x4. Neste tutorial vamos explicar passo a passo, mas, para isso, é necessário que você tenha aprendido a fazer o cubo magico 3x3. Se você precisar de ajuda, você pode dar uma olhada no nosso tutorial.

Você já sabe como fazer o cubo 3x3 e quer enfrentar novos desafios? O cubo magico 4x4 é o próximo em dificuldade. Resolvê-lo é um pouco mais complicado do que o 3x3, pois você terá que aprender novos algoritmos, mas não se preocupe, vamos explicá-los em detalhes.

Para chegar à solução deste cubo vamos usar o método de redução, ou seja, vamos reduzir o 4x4 por um 3x3. Para isso, primeiro faremos os centros, depois as bordas e, assim que chegarmos a esse ponto, resolveremos os cantos como em um 3x3. No entanto, encontraremos novos problemas, como paridades, mas tranquil@, com nossa ajuda você vai resolvê-lo sem problemas. Vamos começar! 

cubo magico 4x4 peças

Assim como o cubo magico 3x3, o cubo 4x4 também é composto por centros, bordas e cantos. No entanto, encontramos algumas diferenças: cada centro é composto por 4 peças, as bordas por 2 e o canto será apenas um. No total teremos:

• 24 peças centrais
• 24 peças que comporão as 12 bordas
• 8 cantos

Cubo Centers 4×4

Bordas do cubo 4×4

Cantos cubos 4×4

Ao contrário dos centros do cubo 3x3, no 4x4 os centros não são fixos. Por isso, devemos ser muito claros sobre qual é a sua posição correta para não ter problemas com a sua resolução.  

Rostos do cubo 4x4

Você notou a cor dos rostos? Da mesma forma que no cubo magico 3x3 encontramos 6 cores, opostas umas às outras. O oposto do branco será amarelo; o oposto de vermelho o laranja eo oposto do verde o azul.

Lembre-se que, para resolver qualquer cubo magico devemos sempre ter uma cara de referência que, no nosso caso, será branca. Desta forma, se levarmos o cubo com o rosto branco para cima, a cor que permanece à nossa direita é vermelha, cujo oposto, como já mencionamos antes, é laranja.

Este é o esquema de cores padrão e é o que encontraremos na maioria dos cubos.

Notação para cubo magico 4x4

Para realizar a cubo magico de 4x4 será necessário conhecer alguma notação, pois é mais provável que veremos casos de paridades que serão resolvidos aplicando certos algoritmos. Para executar esses algoritmos devemos saber o que cada movimento significa. Podemos encontrar:

• No sentido anti-horário: estes são aqueles que serão contrários ao funcionamento do relógio.
• No sentido horário, as voltas que fazemos de acordo com as mãos do relógio.

Cada letra refere-se a um lado do cubo, de modo que:

• U (Up): camada superior
• D (Para baixo): camada inferior
• R (Direita): camada direita
• L (Esquerda): camada esquerda
• F (Frente): camada frontal
• B (Parte traseira): camada traseira

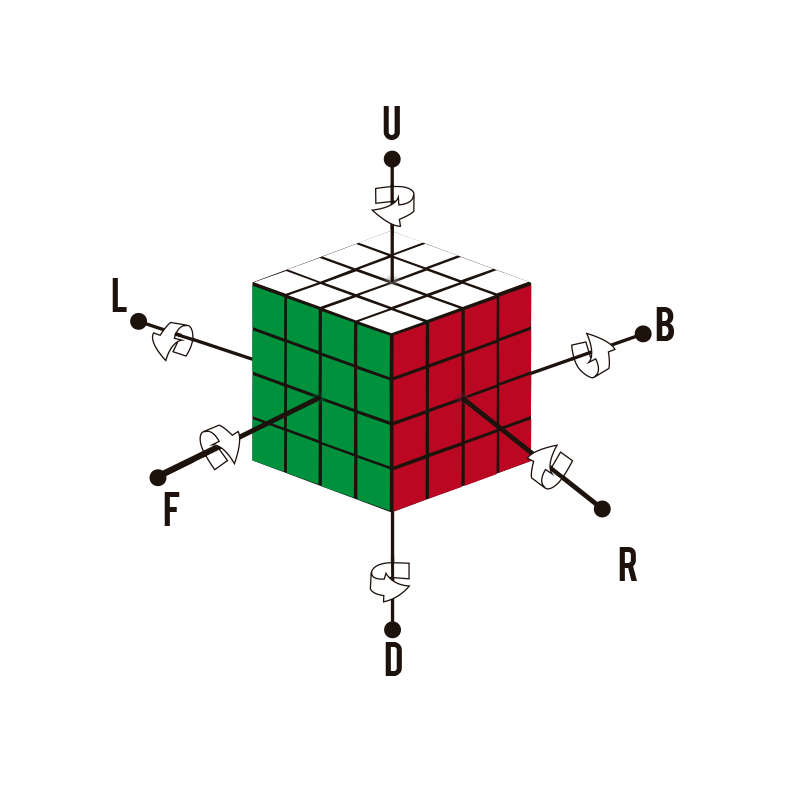
Voltas no sentido horário

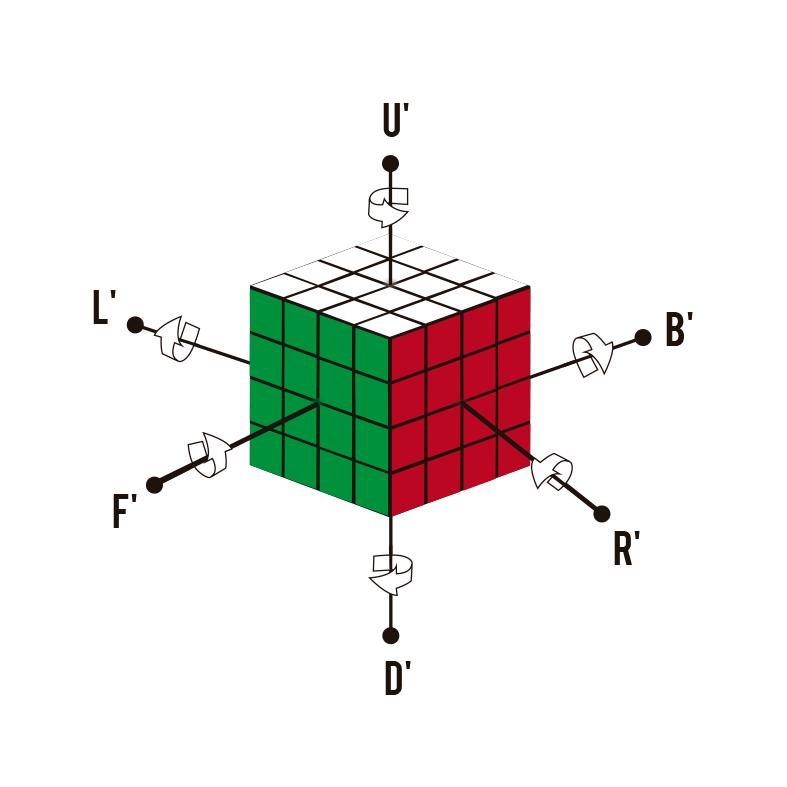
Voltas no sentido anti-horário

Quando você encontra a letra normal, ou seja, sem apóstrofo, significa que a que gira será no sentido horário (U). No entanto, quando ele carrega o apóstrofo, é uma curva anti-horário (U'). Se você ainda tiver alguma dúvida sobre a notação, você pode resolvê-la em nosso artigo onde explicamos toda a anotação do cubo magico. (Você tem o link um pouco abaixo)

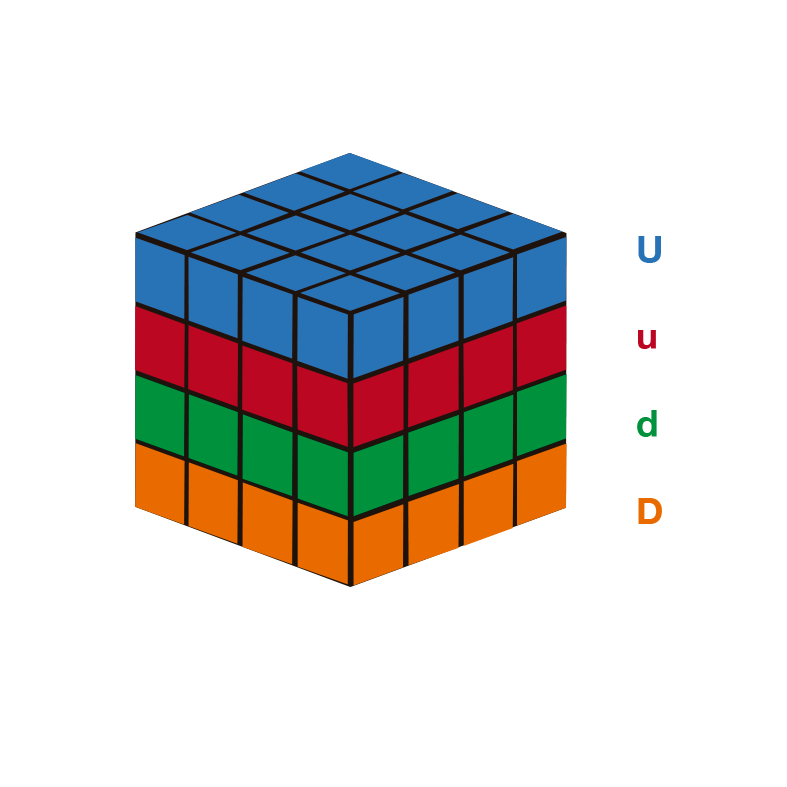
Rotações das camadas internas do cubo 4x4

No 4x4 cubos, além do tempo e voltas anti-horário, há também curvas internas e curvas de duas camadas. Para indicar a rotação das camadas internas, colocaremos a mesma letra da camada externa, mas na minúscula.

Mostramos nas seguintes ilustrações:

Se esta é a sua primeira vez vendo a notação do cubo magico 4x4 você provavelmente precisa de um pouco mais de informação sobre as curvas das camadas. No link a seguir você pode encontrar todas as informações em detalhes.

Passos para resolver o cubo magico 4x4

Resolva os centros

O primeiro passo será resolver os centros do cubo 4x4. Para isso, esqueceremos o resto do cubo porque, a peças central só vai se mover nos centros, ou seja, eles não ocuparão outra posição. Teremos que agrupar cores para que façamos todos os centros. Devemos levar em conta, como acabamos de explicar na seção anterior, a posição das cores.

Para fazer os centros não há algoritmo específico, é feito por intuição. Não se desespere, mesmo que deva muito tempo para reunir a peças... você vai acabar conseguindo! Faremos linhas de dois peças da mesma cor e vamos colocá-las verticalmente para nós para não quebrá-las quando virarmos o cubo. Vamos olhar com cuidado.

• Primeiro centro

O primeiro centro que faremos será o branco.o mais simples de fazer, já que não vamos quebrar nada do que já fizemos, nem temos que construí-lo em qualquer lugar em particular. Nesta etapa, teremos simplesmente que agrupar os quatro peças centrais brancos. Para isso faremos duas linhas brancas emparelhando o peças dois por dois (cada 2 peças formarão uma linha) e vamos nos juntar a eles no mesmo centro.

Agora podemos passar para o próximo centro! Não se preocupe, pouco a pouco você vai praticar.

• Segundo centro

Recomendamos que o próximo centro que você faz depois do branco é o seu oposto, ou seja, amarelo.

Para resolver este centro seguiremos o mesmo método do centro anterior. No entanto, agora devemos ter em mente que, se fizermos qualquer movimento que modifique a peças do rosto branco que colocamos anteriormente, teremos que recuperar essa volta depois de igualar a peças que queremos nos unir formando uma linha. Por exemplo, se eu levantar o rosto certo para juntar dois peças amarelos, depois deste movimento, eu devo proteger os dois peças que eu entrei e retornar a volta da camada direita para recuperar o centro branco.

Posteriormente, devemos inserir a linha no centro correspondente. Por exemplo, temos uma linha amarela de um lado e queremos levantá-la para o lado oposto do branco. A primeira coisa que devemos fazer é, com o centro branco abaixo, colocar a linha verticalmente em nossa visão, elevar o centro para a camada superior, proteger girando a camada duas vezes e retornar o primeiro movimento. Você verá isso mais claramente na imagem a seguir.

Não se preocupe em girar as camadas externas, eles não destruirão o que já fizemos.

Já temos a primeira linha no centro oposto. Agora vamos fazer o segundo emparelhamento das cores e, para elevá-lo, vamos fazer o mesmo algoritmo que na seção anterior, mas vamos colocá-lo sob a linha que já fizemos (linha por linha), para que quando girarmos a camada superior duas vezes e retornarmos o movimento, o centro é feito. Você vai vê-lo melhor na imagem abaixo.

• Terceiro centro

Uma vez que tenhamos feito os dois primeiros centros, colocamos o cubo de lado, para que a cor branca e amarela, respectivamente, permaneça em nosso direito e esquerdo.

O terceiro centro que fazemos pode ser qualquer um. Aquele que vemos que temos mais fácil de construir. Se todos vocês os acharem difíceis, estabeleçam um objetivo e esqueçam o resto. Por exemplo, comece com azul. Pare duas peças azuis e depois outras duas, então você tem duas linhas; lembre-se de colocar as linhas feitas verticalmente em sua visão, de modo a não quebrá-las quando você virar o cubo. Posteriormente, coloque-os no mesmo centro.

Ainda não temos que nos preocupar com a posição das cores, esta é a primeira.

Para isso não há algoritmos, é simples intuição. Não se preocupe, com a prática você vai ver tudo muito mais fácil.

• Sala central

Neste ponto temos que considerar a posição das cores. Você deve levar em conta qual você construiu para colocar os seguintes centros em sua posição correta. Por exemplo, se você construiu o azul, você deve ter em mente que, com o rosto branco para cima, à sua esquerda vai o vermelho e à sua direita o laranja.

Neste caso, vamos fazer o centro vermelho.

Nós colocamos o cubo de volta para que o centro branco e amarelo estejam à nossa direita e esquerda.

Procuramos duas peças vermelhas para que possamos fazer uma linha. Não se preocupe em girar as camadas externas. Eles não vão quebrar nada que fizemos, ao contrário dos internos.

Fazemos a primeira linha e a levamos à sua posição correta ao lado da cor azul. Explicaremos como fazê-lo mais extensivamente no final deste parágrafo, mas resumindo: com o centro branco à nossa direita e a linha vermelha à nossa esquerda, levantamos a linha direita azul para que haja um centro abaixo de onde a linha vermelha está localizada. Em seguida, giramos a camada onde a linha vermelha está localizada, de modo que sua posição é linha ao lado da linha e retornar o centro azul. Agora teremos o centro azul novamente construído e uma linha vermelha em sua posição correta.

Colocando as linhas no quarto centro, podemos encontrar três casos:  

• Primeiro caso: a linha vermelha está localizada no centro que corresponde a ela. Basta girar a camada externa para deixá-la à esquerda e passar para o próximo passo.
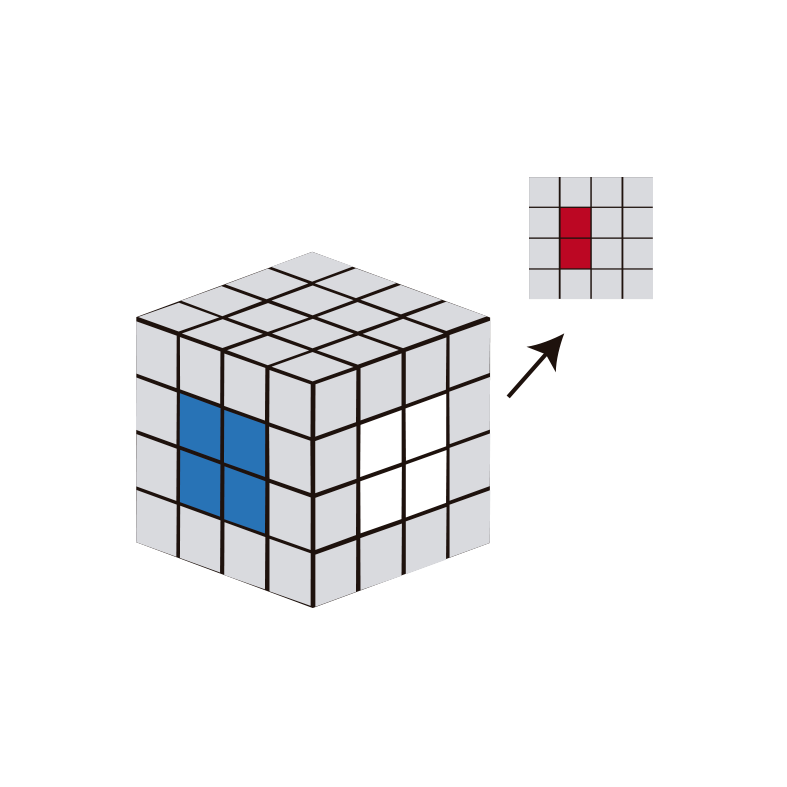
• Segundo caso: a linha vermelha está no lado oposto do azul. Nesta situação, o algoritmo a seguir seria (com o centro branco à nossa direita):
  • Coloque a linha vermelha à sua esquerda.
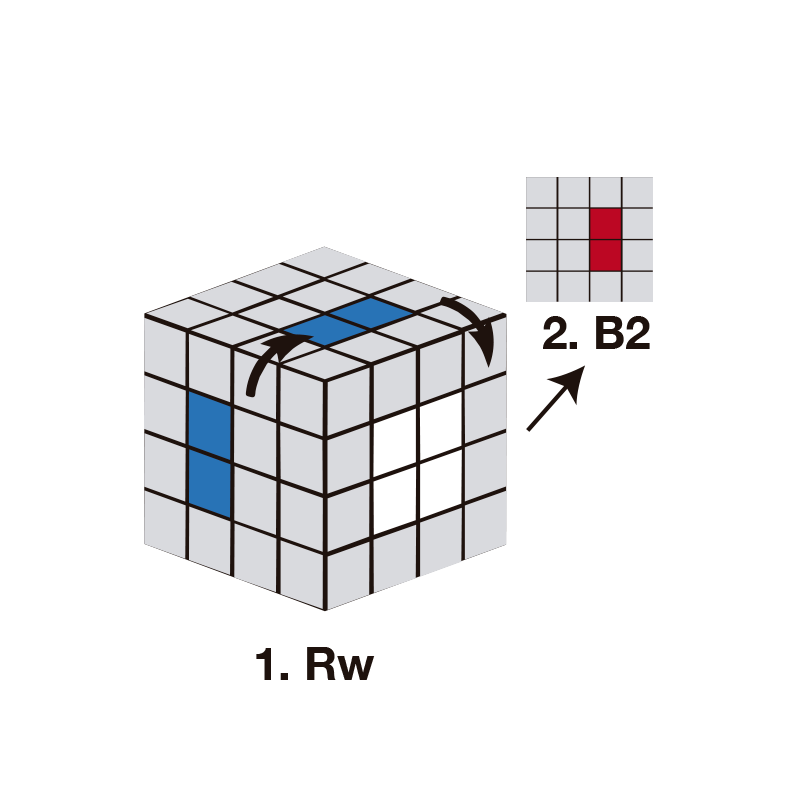
  • Executar o algoritmo: Rw, B2, Rw'. Onde Rw sobe a linha direita azul um centro acima; B2 gira a linha vermelha da esquerda para a direita, para colocá-la ao lado do azul e Rw' retorna o movimento da linha azul e, por sua vez, baixa a linha vermelha para sua posição. Quando estiver no centro, gire a camada onde a linha vermelha está localizada para colocá-la à nossa esquerda (U2).

Se você não esclarece assim, olhe para a imagem abaixo.

Terceiro movimento

Quarto movimento

• Terceiro caso: se a linha vermelha está localizada ao lado da face azul, mas no centro que corresponde ao centro laranja, devemos fazer o mesmo algoritmo que no caso anterior. No entanto, desta vez, em vez de virar a camada direita uma vez, vamos fazê-lo duas vezes. Rw2, B2, Rw2, U2.

Já temos a primeira linha. Vamos com o próximo!

Para colocar a linha que falta, faremos o mesmo, tomando o cuidado de proteger e devolver os movimentos que envolvem quebrar algum centro que fizemos. Uma vez que a linha é formada usamos o algoritmo que fizemos com a primeira linha.

Caso não se lembre bem, lembramos como era esse algoritmo:

Com o centro branco à nossa direita: Colocamos a linha vermelha à nossa esquerda na camada que é, levantamos a linha direita azul (uma ou duas vezes, dependendo de onde a linha vermelha está localizada - deve haver um centro abaixo da nossa linha vermelha-), viramos a camada da linha vermelha duas vezes para que ela fique alinhada com a linha; e, finalmente, devolvemos o movimento.

• Centros 5 e 6

Só temos dois centros para fazer. Para resolver os dois últimos centros, faremos o verde e, pelo descarte, a laranja também será feita. Anime-se, em breve teremos a cubo magico 4x4 resolvida!

Para fazer este centro, primeiro vamos fazer uma linha verde e depois vamos apresentá-la ao lado do centro vermelho. Se ele já estiver colocado em sua posição correta, faremos como antes: colocamos à nossa esquerda e formamos a próxima linha verde.

No entanto, descobrimos que é no centro que corresponde ao laranja, usamos o algoritmo que já conhecemos: Rw, B2, Rw'. Em outras palavras, com o centro branco à nossa direita e a linha verde verticalmente à nossa esquerda, levantamos a camada direita uma vez, viramos duas vezes onde a linha verde está e retornamos o primeiro movimento. Uma vez feito isso, colocamos esta linha à nossa esquerda e fazemos a próxima linha.

Se conseguirmos a última linha de volta à sua posição correta a primeira... ótimo, já resolvemos todos os centros!

Se não, repetiremos os movimentos anteriores. Lembrar. com o centro branco à nossa direita e a linha verde vertical à nossa esquerda, levantamos a camada direita uma vez, viramos duas vezes onde a linha verde está localizada e retornamos o primeiro movimento. Mire bem no algoritmo: Rw, B2, Rw'.

E...é isso! Nós já fizemos todos os centros. Vamos agora ver como resolver as bordas.

Resolver bordas

Esse passo é o mais complicado, pois encontraremos as temidas paridades que caracterizam até mesmo cubos, como é o caso do rubik 4x4. Mas não se preocupe, vamos guiá-lo passo a passo para que você possa resolvê-lo.

Antes de mais nada, para fazer as curvas, é muito importante levarmos em conta que vamos procurá-los horizontalmente, não verticalmente.

Nosso primeiro objetivo será encontrar duas bordas uma virada, mas para que elas não estejam na mesma linha; como mostrado na imagem a seguir.

Caso de bordas voltadas umas para as outras em linhas diferentes

Caso de bordas voltadas umas para as outras em linhas diferentes[/legenda] Se encontrarmos duas bordas, mas na mesma posição (como na imagem a seguir) devemos aplicar este algoritmo para resolvê-lo: (R, U, R', U') F', U, F

Caso de bordas viradas um para o outro na mesma linha

1. Temos duas bordas viradas uma para a outra, mas para que elas não estejam na mesma linha, ou seja, localizadas à direita e à esquerda. Neste caso, executaremos o seguinte algoritmo: (R, U, R', U') F', U, F.

As bordas estão na posição correta para resolução. Ou seja, um na frente do outro, mas em linhas diferentes.

As primeiras bordas.

As primeiras bordas são as mais fáceis de resolver.

Vamos começar colocando o cubo em uma posição de referência, para que ele seja mais confortável de se mover. Nossa posição de referência será o rosto branco para cima e o rosto amarelo para baixo. Desta forma, as bordas que resolveremos serão horizontais para nós no resto das faces do cubo.

Para começar, vamos manter as bordas que estamos fazendo no rosto branco e amarelo. Esta parte é a mais simples e gradualmente se tornará mais complicada.

Colocamos as bordas no caso que já explicamos que nos interessa, uma na frente da outra, mas em linhas diferentes; nós os juntamos e subimos para salvar. Faremos o seguinte:

• Para participar, só teremos que transformar as duas camadas superior ou inferior para um lado.
• Para subir, giramos a camada externa para a direita ou para a esquerda (dependendo de onde temos a borda) para cima; protegemos o movimento e devolvemos.

Depende de onde mantemos a vantagem, vamos executar um algoritmo ou outro:

À direita: Uw', R, U, R', Uw.

Esquerda: Dw', L', U, L, Dw

Na imagem a seguir mostramos um exemplo de como seria se salvasse a borda para a direita com o algoritmo Uw', R, U, R', Uw

Vamos repetir esses mesmos movimentos até que façamos toda a camada do centro branco com bordas que temos bem colocadas. Para fazer isso quando subirmos, devemos sempre tentar baixar uma borda que é mal feita.

Quando tivermos a camada superior com o centro branco com quatro bordas corretas feitas, vamos girar o cubo. e forma, agora a camada do centro amarelo está acima e a do centro branco abaixo.

Continuaremos a fazer bordas como explicamos e colocando-as na camada superior (neste caso o centro amarelo). Não se preocupe em desmontar o cubo, pois as bordas que continuaremos procurando nas camadas centrais, não vamos quebrar o que já fizemos.

Quando você completar as bordas desta camada, a coisa mais complicada começará. Agora, relaxe. Faça isso discretamente, tome seu tempo para procurar o peças na posição que lhe interessa e vá colocar as bordas e, acima de tudo, não desista. É tudo uma questão de prática.

As bordas centrais

Para resolver as bordas centrais, devemos baixar uma das bordas que fizemos ao centro do cubo, para que possamos continuar fazendo bordas como normalmente fizemos e colocando-as acima. Só teremos que fazer esse passo duas vezes; as duas últimas bordas serão feitas ou serão feitas de outra forma.

As duas últimas arestas serão dadas a nós ou teremos que terminá-las de outra forma.

Neste caso, se as duas últimas arestas não tiverem sido dadas a nós, teremos dois casos:

• No primeiro caso, as bordas se enfrentam em linhas diferentes. Nesta ocasião, ao contrário do resto do processo, isso não nos interessa.
• No segundo caso, teremos as duas bordas viradas uma para a outra. Isso será o que vamos procurar.

Se a situação do primeiro caso aparecer, teremos que aplicar o algoritmo de inversão que temos aplicado nessas ocasiões, e isso é explicado acima. Vamos repetir mais uma vez:

Com as duas bordas localizadas à nossa direita e esquerda: R, U, R', U') F', U, F.

Fazendo este algoritmo vamos obter o segundo caso, ou seja, teremos duas bordas voltadas uma para a outra (aquela que nos interessa nesta ocasião). Lembre-se que para colocá-los voltados um para o outro você pode, se necessário, girar as camadas externas. Esses movimentos não vão supor qualquer mudança nem quebrarão qualquer centro ou borda já feita.

Quando conseguirmos colocar uma borda voltada para a outra, aplicaremos um algoritmo que já conhecemos e teremos todos eles prontos. Preparado? Vamos lá!

Teremos que dividir as duas camadas principais fazendo Uw e, em seguida, aplicar o algoritmo de inversão; finalmente retornamos o movimento das camadas superiores e... Voila. O algoritmo é (com as duas bordas localizadas à nossa esquerda e direita): U'w, (R, U, R', U') F', U, F, U, Uw.

Resolução 3x3 com paridades

Nós já fizemos todos os centros e todas as bordas. Agora vem a parte mais fácil e divertida, porque só teremos que resolver o cubo como um 3x3 normal e teremos terminado nosso cubo 4x4.

No entanto, durante o processo podemos encontrar alguns problemas... Você notará que quando você faz a cruz amarela você não recebe o peças para ser colocado em sua posição correta. Muito simples, você está enfrentando um caso de paridade! Mas não entre em pânico... abaixo vamos explicar o que você tem que fazer para resolvê-lo.

Vamos voltar ao início desta parte e começar de novo:

Quando já temos os centros e bordas feitos de nosso cubo magico 4x4, devemos imaginar que nosso cubo é um 3x3. Você sabe como resolver um 3x3, certo? Bem, aplique seus algoritmos para fazer a cruz branca, em seguida, coloque os cantos, em seguida, as bordas centrais e, finalmente, fazer a última camada. Poço... talvez seu método seja de outra forma, faça como você sabe e será mais confortável para você!

Ao fazer a última camada pode haver quatro casos:

1. CASO 1: RESOLVIDO

Na melhor das hipóteses você pode fazer e terminar seu cubo sem problemas. Se essa é a sua situação... Parabéns, você já terminou sua 4x4 e você não veio com nenhuma paridade! Se não for... Ler.

2. CASO 2: PARIDADE OLL

Você está fazendo a cruz amarela e você encontra uma borda que é virada. Você veio com paridade OLL! Quando fazemos a cruz amarela em um 3x3 encontramos quatro casos: o ponto, uma borda, a linha e um L, que é comumente chamado de "Las 9". Bem, se você quiser reconhecer o primeiro se vamos ter que executar um algoritmo OLL em nosso 4x4, fazer a cruz amarela será orientado ou uma única borda ou o L; ou seja, um número ímpar de bordas orientadas.

Para resolver o caso de paridade ao mesmo tempo que você vê-lo, use o algoritmo de Paridade OLL. Não importa de que borda você comece a aplicar o algoritmo, ele será removido de onde quer que você faça; mas o ideal seria que você começasse na borda que tem paridade. O algoritmo é o seguinte:

OLL Parity: Rw, U2, (x) Rw, U2, Rw, U2, Rw' U2, Lw, U2, Rw' U2, Rw, U2, Rw' U2, Rw'

Exemplo de Paridade OLL

3. CASO 3: PARIDADE PLL

Você encontra dois peças trocados juntos. Isso significa que ele tem duas bordas boas e duas ruins. Outra paridade! Desta vez é o PLL e é mais fácil de resolver do que o anterior.

Também podemos encontrar todas as bordas bem e dois cantos mal. Não se preocupe, está resolvido com o mesmo algoritmo.

Em conclusão, você terá dois peças trocados juntos, sejam bordas ou cantos; e o algoritmo com o qual ele é resolvido é o seguinte.

Paridade PLL: r2, U2, r2, Uw2, r2, Uw2  

Exemplo de Paridade PLL

4. CASO 4: PARIDADE DUPLA

O último caso que podemos encontrar será no qual os dois tipos de paridades aparecem juntos; a de OLL e PLL. Não se preocupe, os algoritmos são os mesmos que acabamos de aprender e executamos na seguinte ordem:

Em primeiro lugar, a OLL é feita porque será a primeira e, finalmente, a PLL. Uma vez executados ambos os algoritmos, resolveremos o cubo pelo nosso método habitual.

Nós já fizemos nosso 4x4!!. Agora você só terá que praticar muito e logo você vai resolvê-lo sem problema.

Achou difícil? Se preferir, você pode contar com nossos tutoriais em vídeo. Nelas explicamos tudo o que é lido acima.

Vídeo para resolver o cubo magico 4x4

Vídeo para resolver paridades

E... Se você ainda tiver alguma dúvida depois de ler o tutorial e assistir aos vídeos, escreva-nos um comentário e tentaremos respondê-lo o mais rápido possível.

Resolvê-lo!